近日,77779193永利集团刘剑课题组在美国化学会杂志《化学研究述评》 (Accounts of Chemical Research)发表了邀稿综述文章https://doi.org/10.1021/acs.accounts.1c00511 ,总结了该课题组在非绝热动力学的相空间映射理论和计算方法的系列进展。
什么是非绝热动力学?我们就要从绝热过程说起,它最初指热力学中系统与环境之间没有热交换的过程。在量子力学中,如果一个电子处于确定的能态上保持概率分布恒定而没有交换,这种过程称为电子绝热过程,或者称玻恩-奥本海默近似。然而当两个或多个电子态势能面非常接近时,电子与原子核的运动(振动和转动)耦合,致使不同电子态上的布居数发生变化,这也就是所谓的非绝热过程。非绝热过程广泛存在于化学、生物和材料领域,如许多常见的光化学反应、材料中的光电转换过程、微腔光场化学、视网膜成像和DNA光损伤/光修复等生物化学反应。发展适合全原子模拟的非绝热动力学理论方法来研究实际凝聚态体系非绝热过程的微观变化和行为一直是当代物理化学的一个热点和难点。
图1. 刘剑课题组发展的非绝热动力学相空间映射理论方法在化学领域的一些应用
为了克服非绝热动力学中“维数灾难”问题(常见于量子波包动力学方法),我们希望在量子相空间的框架下借助轨迹近似发展非绝热动力学方法,这样对于大体系的非绝热过程模拟可以具有线性标度的性质。然而电子的运动如何与原子核的轨迹匹合,一直是非绝热轨迹动力学中存在的一个问题,比如传统轨迹近似方法如埃伦费斯特(Ehrenfest)动力学或面跳跃(Surface Hopping)动力学在凝聚相体系的计算中都不尽如意,且欠乏坚实的理论根基。如果可以将电子的自由度也映射到相空间,于是电子就与原子核一样可以在相空间的轨迹图像下统一演化。映射方式就如同搭 “皮影戏” ,使得我们可以通过研究相空间虚拟准粒子 “影像” ,来刻画真实非绝热过程的量子对象。
2016年,刘剑课题组提出了多电子态哈密顿量的统一映射框架(Journal of Chemical Physics, 2016, 145, 204105 http://dx.doi.org/10.1063/1.4967815 )。该工作通过将福克(Fock)空间内的产生-湮灭算符与泡利(Pauli)算符作对映,自然推导出包括传统Meyer-Miller 映射哈密顿量等一系列映射模型,建立基于量子经典对应下对纯电子自由度的映射框架。2019年,该课题组在此基础上提出将电子态空间单位算符与映射相空间中的单位1的对应关系作为约束条件来发展新的相空间非绝热动力学方法,称为经典映射模型(classical mapping model, CMM) (Journal of Chemical Physics, 2019, 151, 024105 https://doi.org/10.1063/1.5108736 )。CMM首次在约束相空间(高维约束球面)下讨论映射问题,能够在凝聚相体系中拿到远胜于传统的埃伦费斯特动力学或面跳跃方法的结果。
2021年,该课题组进一步发展了量子相空间映射理论(Journal of Physical Chemistry Letter, 2021, 12, 2496−2501 https://pubs.acs.org/doi/full/10.1021/acs.jpclett.1c00232 ),使用了恰当的数学映射变换核一致地刻画了(原子核)连续自由度的相空间和(电子)离散自由度的相空间,其中离散空间的相空间将自然导出约束关系。该课题组发现离散态的相空间映射核中零点能参数γ仍可以在 (-1/F, ∞) 内选取(都保持严格映射关系),基于此的经典轨迹近似也称为扩展的CMM (eCMM)。γ的取值包括负值,这就不同于40多年来一直将其视作零点能参数的思想,结果表明负值的γ在低温、快热库、强耦合的自旋玻色模型中能够给出更合理的近似,同时原则上也避免了映射动力学中势能面翻转问题。
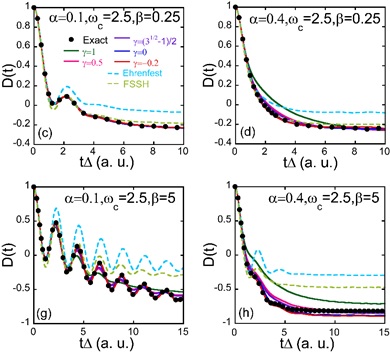
图2. 对自旋-玻色模型布居数转移的模拟结果
该课题组的后续工作指出相空间映射模型中的准粒子的位置算符和动量算符的对易关系其实不一定满足传统的海森堡不确定原理(玻恩正则对易关系),而是一般存在对易子矩阵,在此基础上可以得到一种更为广泛的映射哈密顿量形式(Journal of Physical Chemistry A, 2021, 125, 6845−6863 https://doi.org/10.1021/acs.jpca.1c04429 )。将对易子变量满足玻恩-奥本海默极限约束条件,作者由此发展的eCMMcv方法成功计算了多电子态散射模型、光解离模型、蛋白复合物凝聚相耗散体系以及光腔中原子体系等谐性或非谐性模型的非绝热动力学结果。
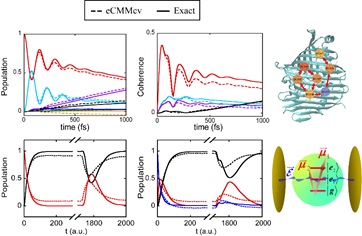
图3. 对蛋白复合物耗散体系和微腔光场与原子相互作用模型的模拟结果
参与上述系列课题的人员包括77779193永利集团2019级研究生贺鑫和吴柏华,以及博雅博士后龚志浩。北京大学77779193永利集团、永利集团科学与工程计算中心刘剑为通讯作者。以上课题得到国家自然科学基金委、科技部、北京分子科学国家研究中心的资助,以及北京并行科技、广州超算中心和永利集团高性能计算平台提供的计算资源的协助。