2024年5月15日,美国化学会杂志The Journal of Physical Chemistry Letters在线发表了77779193永利集团刘剑课题组题为“Nonadiabatic Field with Triangle Window Functions on Quantum Phase Space”的文章。该文将刘剑课题组在The Journal of Physical Chemistry Letters, 2024, 15, 644-658 这篇文章中提出的非绝热场(nonadiabatic field, NaF)动力学与基于三角窗函数的时间关联函数计算表达式相结合,提出了三角窗函数非绝热场(NaF-TW)方法。该方法有望为非绝热跃迁动力学计算提供更为可靠与实用的工具。
非绝热跃迁动力学在自然或人工复杂分子系统中涉及光致驱动、光致发射、电子/空穴转移和量子腔体调制等现象或过程中有着重要作用。在非绝热跃迁动力学中,电子态间的跃迁和原子核运动之间在时间尺度上不可分离,两者的动态关联至为关键。传统的平均场方法不能可靠描述渐进区域的分叉现象,而面跳跃方法无法胜任大范围非绝热耦合区域动力学特征的准确刻画。自2016年以来刘剑课题组的一系列工作推广了量子力学相空间表示,提出了约束坐标-动量相空间(CPS)来表示离散的电子态自由度,同时采用传统魏格纳(Wigner)相空间描述连续的原子核自由度,发展出严格的、统一的映射相空间理论,平等地处理电子态和原子核自由度。相较于传统相空间表示,CPS对于描述表示有限(电子)态量子系统的离散(电子)自由度,具有数值计算稳定且高效的天然优越性。刘剑课题组指出基于轨线的非绝热动力学方法包含三个要素:1)运动方程;2)初始值条件;和3)含时物理量的积分表示。量子相空间严格映射理论可以为这三个基本要素的自洽定义提供坚实的基础。刘剑课题组近期基于位置-动量相空间的统一理论,发展出非绝热场(NaF)方法,能够同时可靠地模拟渐进区域和大范围非绝热耦合区域的原子核-电子自由度的动态关联,解决这个领域的一个瓶颈问题,有望为实际复杂分子体系的非绝热跃迁过程提供一种实用线性标度计算方法。
由于CPS表示提供了一个理论框架和数学工具,可针对有限态量子系统推导出更多新的同构表示。刘剑课题组近期在Chinese Journal of Chemical Physics, 2024, 37, 230-254这篇文章中基于CPS表示,采用非协变相空间函数、含时权重函数与含时归一化因子,提出一类可严格推导出两态量子系统(TSS)布居数动力学的新的同构表示。该类同构表示导出的每条轨线对电子态布居数动力学所对应的布居-布居关联函数的贡献严格半正定。针对该类表示,经过一系列积分变量代换,证明了电子态布居数严格动力学与含时归一化因子的某类轴对称相对应。严格解出该轴对称所给出的阿贝尔积分方程,即可推导出对应两态系统严格布居数动力学的这类同构表示的解析形式。自2016年Cotton和Miller于The Journal of Chemical Physics, 2016, 145, 144108 这篇文献中提出以来,三角窗函数(TW)方法一直被认为只是一种经验性方法。令人振奋的是,刘剑课题组提出的这类同构表示自然地涵盖了三角窗函数方法,从而证明了三角窗函数方法本质上是两态系统布居数动力学的一种严格表示。
鉴于三角窗函数方法满足布居数动力学的半正定性质并且严格同构于两态系统的布居数动力学,该文期望将三角窗函数方法进一步应用于涉及原子核运动的耦合多电子态系统的非绝热动力学。在Chinese Journal of Chemical Physics, 2024, 37, 230-254这项工作的基础上,该文基于CPS表示和三角窗函数形式,采用了Cotton与Miller在The Journal of Chemical Physics, 2019, 150, 104101 这篇文献给出的布居-布居关联函数的定义,同时更进一步定义了有限电子态系统的布居-相干、相干-布居与相干-相干关联函数的严格同构映射形式。将以上关联函数形式与刘剑课题组提出的非绝热场(NaF)轨线动力学结合,可模拟同时含电子与原子核自由度的化学体系的动态行为,该文将其称为三角窗函数非绝热场(NaF-TW)方法。
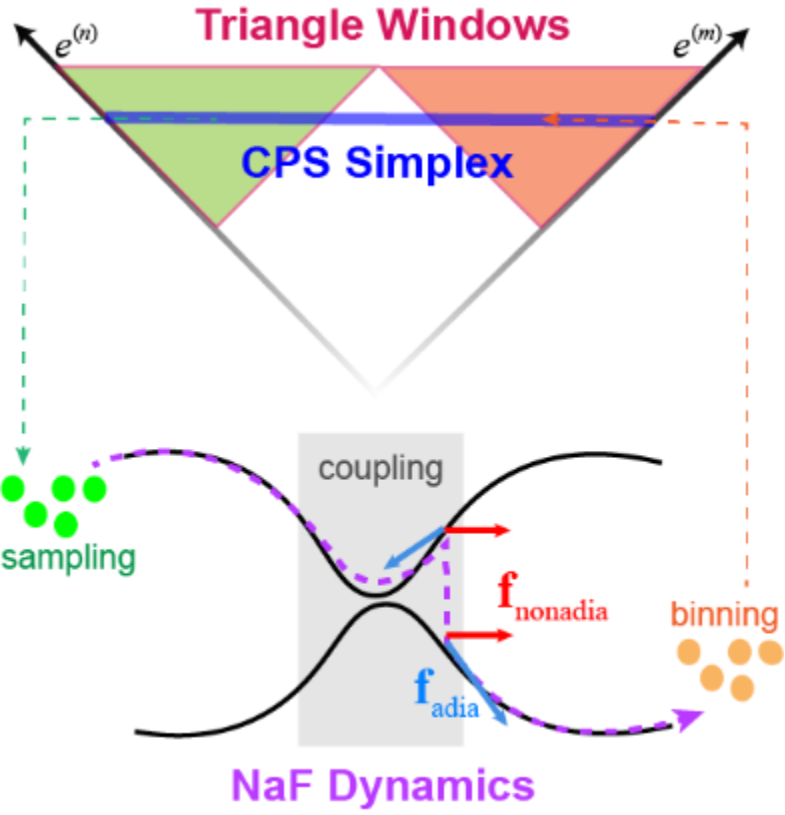
图1:三角窗函数非绝热场(NaF-TW)方法示意图。
对比目前两类主要的(独立)轨线动力学方法:一类是基于瞬时跃迁转移近似连接不同单绝热态势能面(PES)生成的玻恩-奥本海默(BO)轨线所发展出的面跳跃(Surface Hopping)动力学;另一类方法则依据1927年埃伦费斯特(Ehrenfest)定理的精神,采用原子核在平均势能面上运动的平均场动力学近似图像。与以上两类传统非绝热动力学方法概念上不同的NaF方法将轨线近似中的原子核受力分为两项:除包含在单一电子态势能面上的绝热力外,还包含一项重要的非绝热力。NaF方法在根本思想上与上述两类传统方法有显著区别,能够更可靠地描述原子核运动和电子之间的动态相互作用,并自然地捕捉到原子核运动行为在非绝热耦合区域与非绝热耦合消失区域的变化。
在该文中,刘剑课题组发展的NaF-TW方法突破了Cotton和Miller基于平均场动力学所提出的对称准经典TW方法(SQC-TW)的局限:它不仅确保了电子态布居-布居关联函数的半正定性,并且较为准确地同时刻画了电子和原子核自由度的动力学,可以描述好从渐进区域到大范围非绝热耦合区域的广泛区域,胜任从气态到凝聚态化学体系的非绝热动力学模拟。
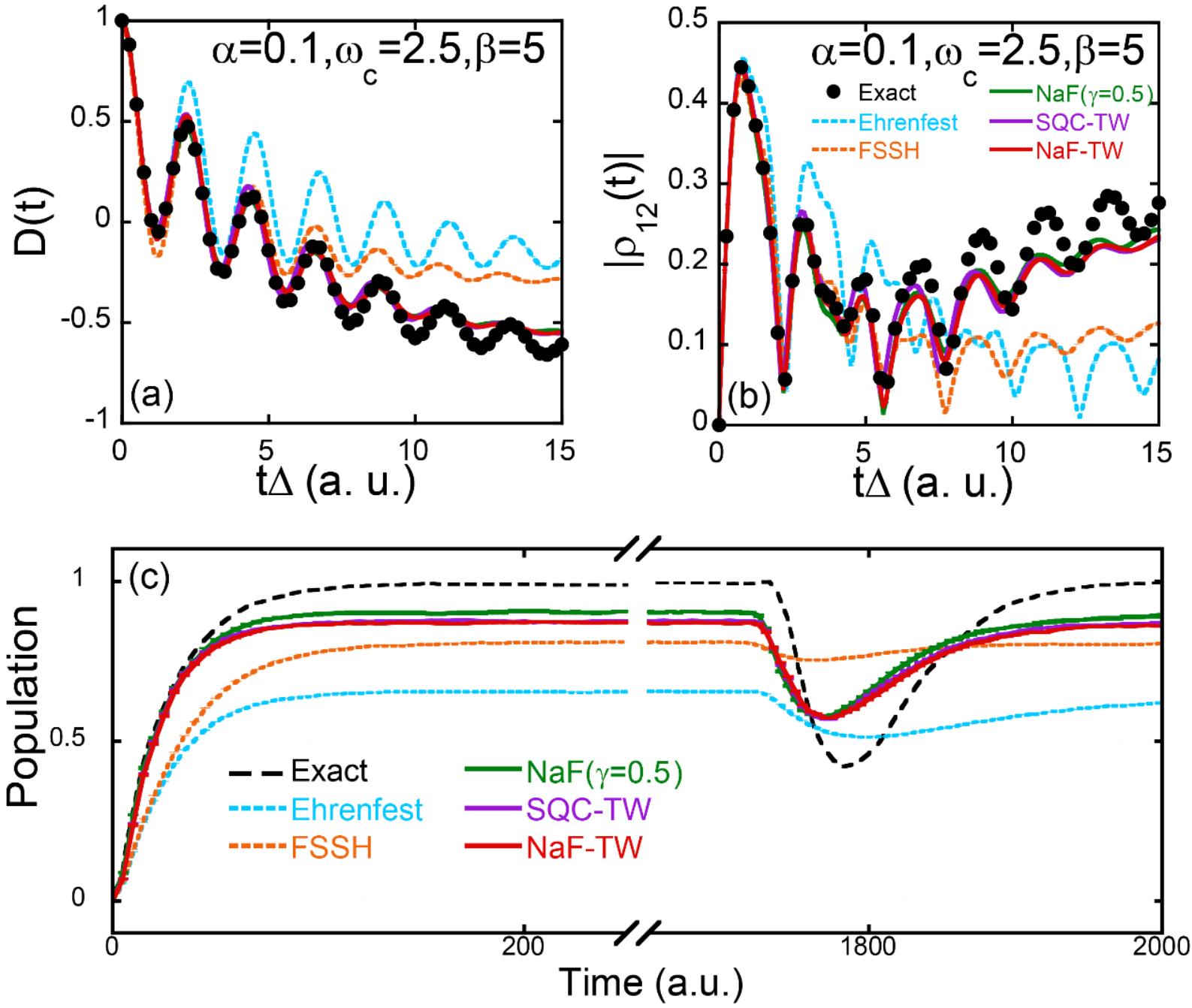
图2:在两态模型中,我们对比了NaF-TW、SQC-TW、NaF(采用CPS)、Ehrenfest动力学以及FSSH(最少面跳跃)的结果:(a) 展示了自旋玻色模型中的电子态布居数之差的动力学,(b) 显示了自旋玻色模型中的密度矩阵非对角元模的动力学,而(c) 则呈现了两能级的原子-光腔模型的布居数动力学结果。
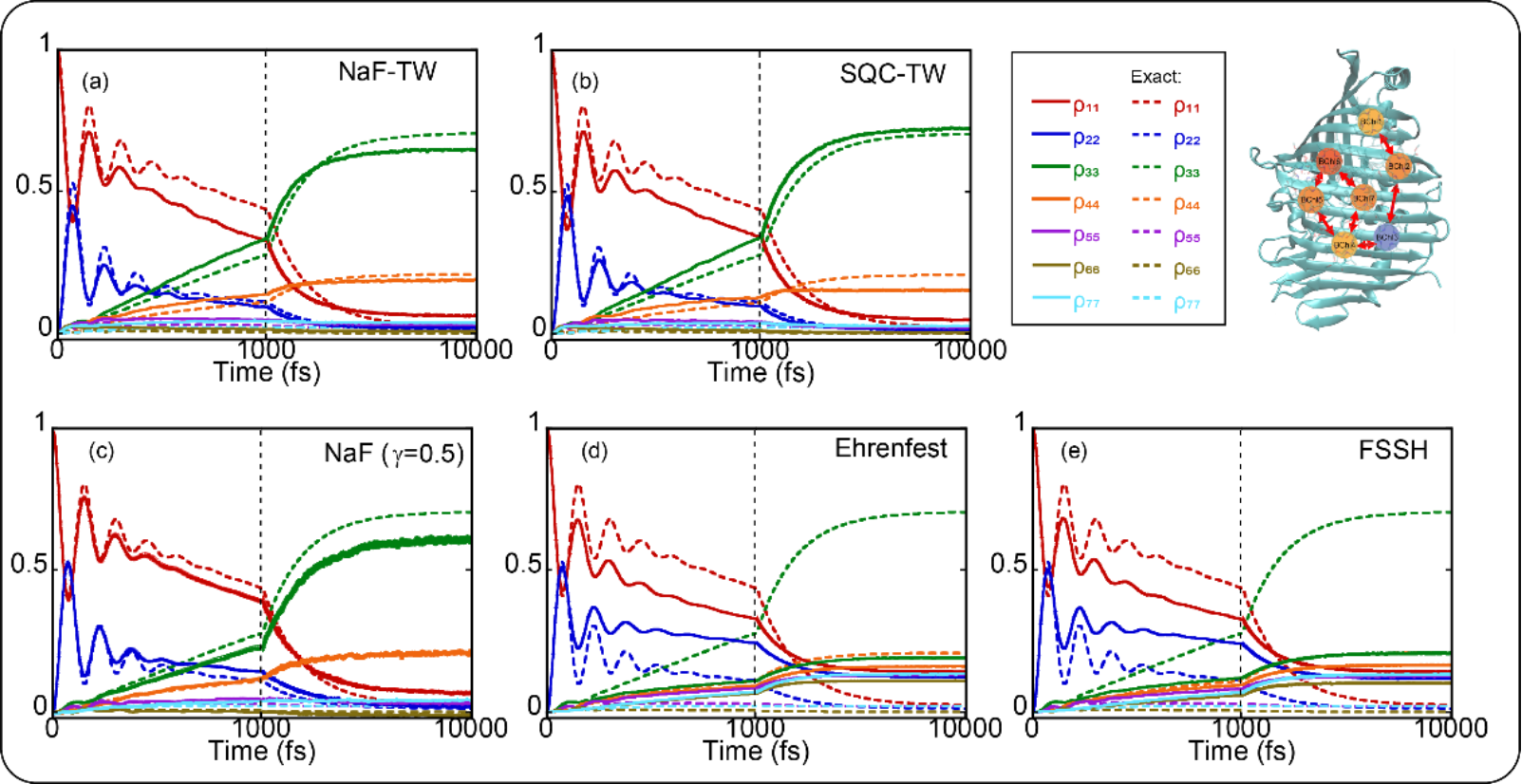
图3:(a)-(e)分别展示了在七态FMO模型中采用的布居数动力学结果,其中(a)为NaF-TW,(b)为SQC-TW,(c)为NaF(采用CPS),(d)为Ehrenfest动力学,(e)为FSSH。
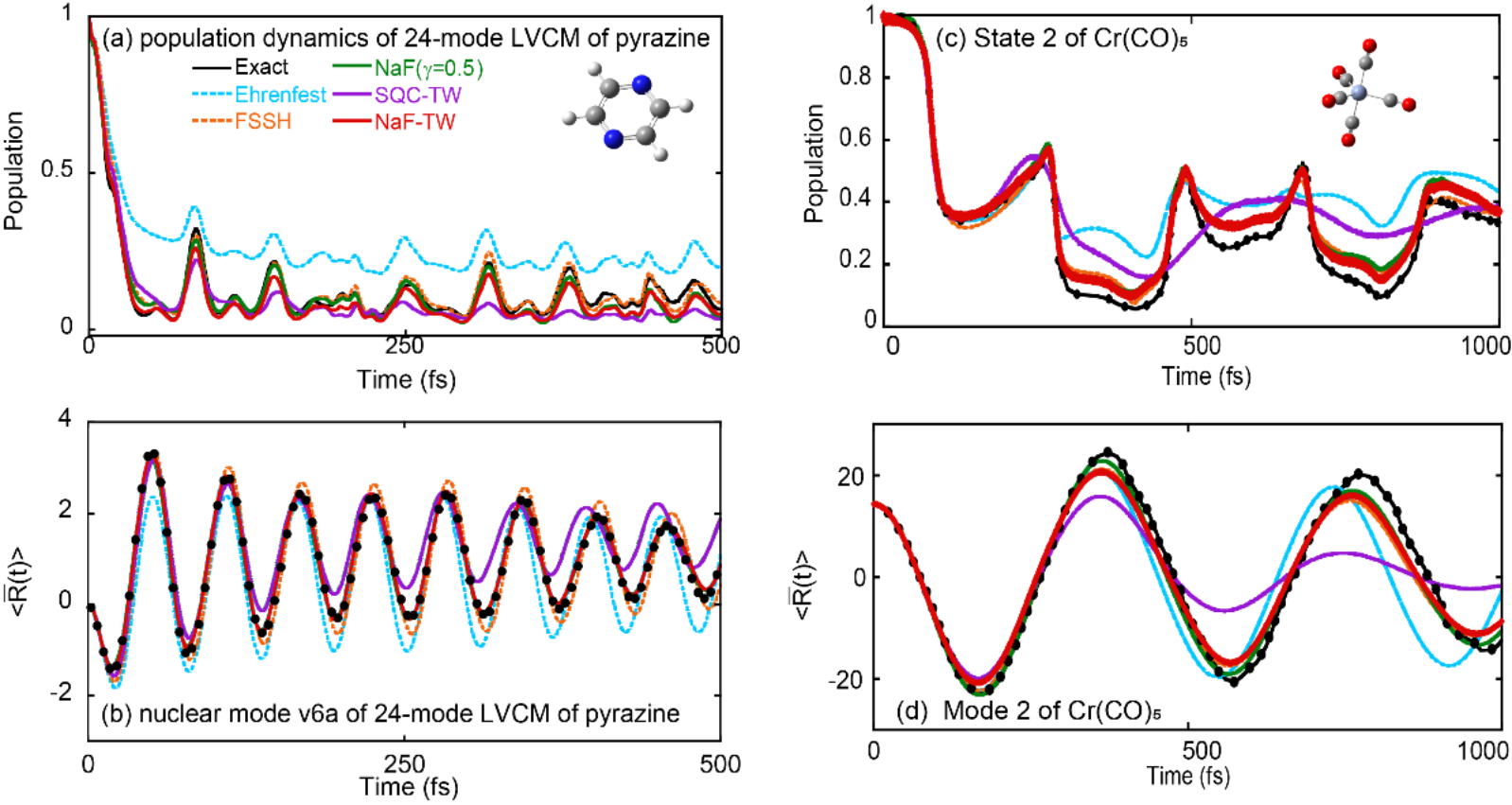
图4:(a)-(b)展示了NaF-TW、SQC-TW、NaF(采用CPS)、Ehrenfest动力学以及FSSH在24模-2态的吡嗪分子经过锥形交叉过程中的布居数动力学以及简正模位置期望随时间的变化。(c)-(d)对应着3态的Cr(CO)5分子经过锥形交叉过程中的布居数动力学以及简正模位置期望随时间的变化。
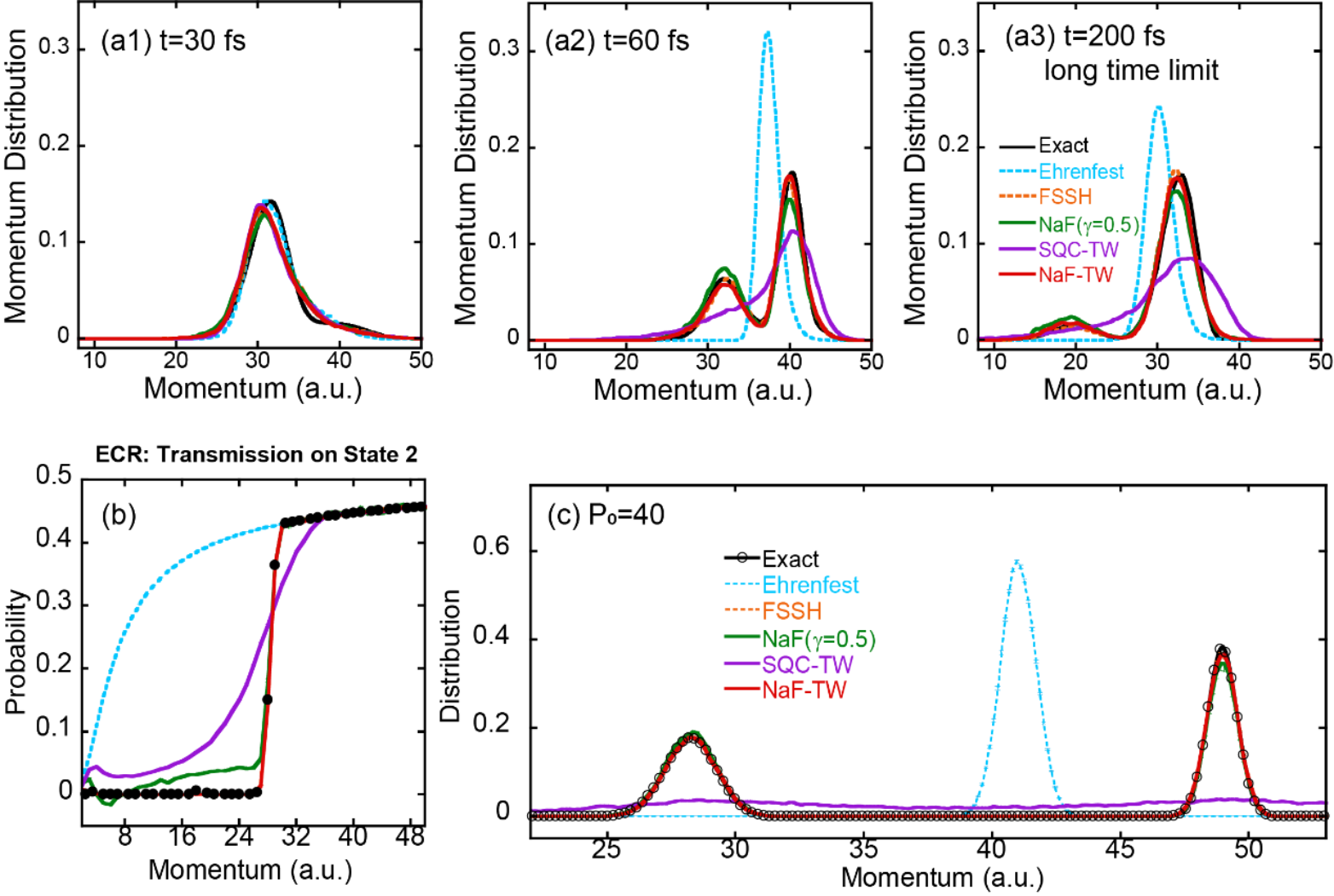
图5:(a1)-(a3)分别展示了NaF-TW、SQC-TW、NaF(采用CPS)、Ehrenfest动力学以及FSSH在三态Morse势光解离动力学中原子核动量分别在t=30fs、60fs以及200fs时的分布情况。(b) 描述了上述不同方法在Tully的ECR散射模型中,隧穿在第二个态上的概率随着入射动量分布中心值的变化曲线。(c) 对应于上述不同方法在Tully的ECR散射模型中入射动量分布中心值为40a.u.时的动量分布情况。
上述图2和图3展示了不同非绝热轨线方法对凝聚相体系计算结果的对比,表明基于CPS相空间与TW方法的各种时间关联函数计算在数值表现上显著性地优于Ehrenfest动力学和FSSH这两类传统方法。图4展示了不同方法在实际分子的锥形交叉模型上的对比,NaF、NaF-TW以及FSSH要优于SQC-TW和Ehrenfest动力学。最后,图5展示了不同方法针对气相模型的计算结果,显示了NaF-TW相比于SQC-TW在描述原子核的动力学性质上更具优势。
刘剑课题组将CPS表示和三角窗函数(TW)相联系,提出了更加准确的基于三角窗函数的电子态自由度时间关联函数映射形式,并与非绝热场(NaF)方法相结合,建立了三角窗函数非绝热场(NaF-TW)方法。NaF-TW方法既满足电子绝热态布居数动力学的半正定性,又克服了平均场动力学和面跳跃动力学两类传统非绝热动力学方法的局限。NaF-TW方法在理论上更自洽,在一系列从气相到凝聚相的基准测试中的数值表现更优异。这些进展有望为理解和预测自然或人工复杂分子体系中的重要非绝热跃迁过程提供新的可靠、有效工具。
永利集团博士研究生贺鑫、程祥松、吴柏华为文章合作作者,刘剑教授为通讯作者。该工作得到了国家杰出青年科学基金项目(项目号: 22225304)的资助。计算资源由北京并行科技、广州超级计算中心以及永利集团高性能计算平台提供。
文章信息
“Nonadiabatic Field with Triangle Window Functions on Quantum Phase Space”
Xin He, Xiangsong Cheng, Baihua Wu, Jian Liu*. The Journal of Physical Chemistry Letters. 2024, 15, 5452–5466
https://doi.org/10.1021/acs.jpclett.4c00793
“A Novel Class of Phase Space Representations for the Exact Population Dynamics of Two-State Quantum Systems and the Relation to Triangle Window Functions”
Xiangsong Cheng, Xin He, Jian Liu*. Chinese Journal of Chemical Physics. 2024, 37, 230-254